CENTROID OF AN AREA
Engineering Mechanics EME-102
Geometrical Center of an area (A) is often termed as Centroid or Center of an Area.
Suppose we have an area A in a certain X-Y coordinate system, we divide the area into n parts and named them as A1, A2, A3, .... An,. Let the coordinates of those tiny elemental areas are as (X1,Y1), (X2,Y2), (X3,Y3) ..... (Xn,Yn).
Like other vectors, an area has a moment about an axis and be represented by the product of the radial distance between the area and the axis and the area itself. So if an elementary area A1 has a coordinate (X1,Y1) it means the area is at a distance X1 from the Y axis and Y1 from the X axis. Therefore the moment produced by A1 about Y axis is X1A1 and about X axis is Y1A1.
Therefore the summation of all the moments produced by each and every elemental area about Y axis will be ∑AiXi and about X axis will be ∑AiYi.
Again, the resultant area A passes through the point G(Xg,Yg). Therefore the moment produced by the area A about Y axis will be AXg and about X axis will be AYg.
Like other vectors, it will obey the Moment Theorem which states the total moment produced by individual vectors will be exactly equal to the moment produced by the resultant vector about a certain axis.
Therefore,
AXg = A1X1 + A2X2 + A3X3 + ...... + AnXn
and
AYg = A1Y1 + A2Y2 + A3Y3 + ...... + AnYn
For an area, a centroid G(Xg,Yg) can be defined using calculus by the equations,
Xg = (1/A)∫x.dA ------ (i)
Where dA = elemental area and A= total area.
Yg = (1/A)∫y.dA ------ (ii)
HOW TO DERIVE THE VALUES OF Xg and Yg FOR BASIC GEOMETRIC FIGURE:
STEPS TO FIND Xg

i) Draw the figure in a Coordinate System.
ii) Draw a thin strip of area of thickness (dx) parallel to Y axis and at a distance (x) from Y axis.
iii) Find the height of the strip. Either the height will be constant or the height is a function of (x), that can be calculated from the equation of the figure.
iv) Calculate the elemental area of the strip, and named as dA. Hence, dA = hdx
v) integrate the expression ∫xdA, but dA = hdx. Therefore, we shall integrate ∫hxdx over the total area.
vi) Xg = (∫ xdA)/A = (∫ hxdx)/A ; where A = total area = ∫dA = ∫hdx
STEPS TO FIND Yg
i) Draw the figure in a Coordinate System.
ii) Draw a thin strip of area of thickness (dy) parallel to X axis and at a distance (y) from X axis.
iii) Find the length (b) of the strip. Either the length will be constant or the length is a function of (y), that can be calculated from the equation of the figure.
iv) Calculate the elemental area of the strip, and named as dA. Hence, dA = bdy
v) integrate the expression ∫ydA, but dA = bdy. Therefore, we shall integrate ∫bydy over the total area.
vi) Yg = (∫ ydA)/A = (∫bydy)/A
CENTROID OF A COMPOSITE AREA:
HOW TO FIND THE CENTROID OF A COMPOSITE AREA
(a composite area consists of several straight or curved lines.)
(i) Draw the figure in a coordinate system. Draw the dimensions too. Every dimensions will be measured with respect to origin of the coordinate system
(ii) Divide the composite area into several parts of basic geometric areas. Lebel them as part-1, part-2, part-3, .......part-n. Let the corresponding areas are A1, A2, A3, .... An. Let the centroids are G1(X1,Y1), G2(X2,Y2), G3(X3,Y3), ...... Gn(Xn,Yn).
(iii) Let the centroid of the composite area be G(Xg,Yg). Hence,
Xg = (A1X1 + A2X2 +A3X3)/(A1 + A2 + A3)
Yg = (A1Y1 + A2Y2 +A3Y3)/(A1 + A2 + A3)
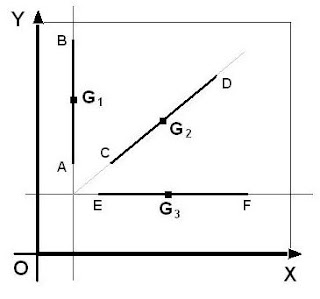
 (a) Suppose we have certain area of magnitude (A) in a coordinate system. The centroid of the area will be at its mid-point. A centroid is denoted by G.
(a) Suppose we have certain area of magnitude (A) in a coordinate system. The centroid of the area will be at its mid-point. A centroid is denoted by G.In the figure we have a complex geometrical area composed of three basic geometrical areas. A rectangle, a semi circle and a isosceles triangle. Let us denote the centroids as G1, G2, G3 for the given areas in the figure.
We shall have to find the Centroid of the entire area composed of A1, A2, A3.
At first, the composite line is divided into three parts.
Part -1 : The semi-circle : Let the centroid of the area A1 be G1(X1,Y1)
Area, A1 = (π/2)x(25)² mm² = 981.74 mm²
X1 = { 25 - (4x25)/(3xπ)} mm = 14.39 mm
Y1 = 25 mm
Part -2 : The Rectangle : Let the centroid of the A2 be G2(X2,Y2)
Area, A2 = 100 x 50 mm² = 5000 mm²
X2 = 25 + (100/2) = 75 mm
Y2 = 25 mm
Part -3 : The Triangle : Let the centroid of the area Area, A3 be G3(X3,Y3)
Area, A3 = (1/2) x 50 x 50 mm² = 1250 mm²
X3 = 25 + 50 + 25 = 100 mm
Y3 = 50 + (50/3) = 66.67 mm
If the centroid of the composite line be G (Xg,Yg)
X1 = { 25 - (4x25)/(3xπ)} mm = 14.39 mm
Y1 = 25 mm
Part -2 : The Rectangle : Let the centroid of the A2 be G2(X2,Y2)
Area, A2 = 100 x 50 mm² = 5000 mm²
X2 = 25 + (100/2) = 75 mm
Y2 = 25 mm
Part -3 : The Triangle : Let the centroid of the area Area, A3 be G3(X3,Y3)
Area, A3 = (1/2) x 50 x 50 mm² = 1250 mm²
X3 = 25 + 50 + 25 = 100 mm
Y3 = 50 + (50/3) = 66.67 mm
If the centroid of the composite line be G (Xg,Yg)
Xg = (∑AiXi)/(∑Ai)
= (A1X1 + A2X2 +A3X3)/(A1 + A2 + A3)
= (981.74 x 14.39 + 5000 x 75 + 1250 x 100)/( 981.74 + 5000 + 1250)
= 71.09
Yg = (∑AiYi)/(∑Ai)
= (A1Y1 + A2Y2 +A3Y3)/(A1 + A2 + A3)
= (981.74 x 25 + 5000 x 25 + 1250 x 66.67)/ ( 981.74 + 5000 + 1250)
= 32.20