CENTROID OF AN AREA

 

CENTROID OF AN AREA

Engineering Mechanics EME-102

Geometrical Center of an area (A) is often termed as Centroid or Center of an Area.

Suppose we have an area A in a certain X-Y coordinate system, we divide the area into n parts and named them as A₁, A₂, A₃, .... A_n,. Let the coordinates of those tiny elemental areas are as (X₁,Y₁), (X₂,Y₂), (X₃,Y₃) ..... (X_n,Y_n).

As area can be represented by a vector, hence, Area A can be treated as the resultant of the tiny elemental vectors A₁, A₂, A₃, .... A_n... Let the direction of the resultant vector passes through the point G(X_g,Y_g) on the plane of the area. The point G(X_g,Y_g) is called the CENTROID of the area A. (The direction of any area is along the perpendicular to the area drawn at the centroid of the area).

Like other vectors, an area has a moment about an axis and be represented by the product of the radial distance between the area and the axis and the area itself. So if an elementary area A₁ has a coordinate (X₁,Y₁) it means the area is at a distance X₁ from the Y axis and Y₁ from the X axis. Therefore the moment produced by A1 about Y axis is X₁A₁ and about X axis is Y₁A₁.

 Therefore the summation of all the moments produced by each and every elemental area about Y axis will be ∑A_iX_i and about X axis will be ∑A_iY_i.

Again, the resultant area A passes through the point G(X_g,Y_g). Therefore the moment produced by the area A about Y axis will be AX_g and about X axis will be AY_g.

Like other vectors, it will obey the Moment Theorem which states the total moment produced by individual vectors will be exactly equal to the moment produced by the resultant vector about a certain axis.

Therefore,
AX_g = A₁X₁ + A₂X₂ + A₃X₃ + ...... + A_nX_n

and
AY_g = A₁Y₁ + A₂Y₂ + A₃Y₃ + ...... + A_nY_n

           

                 For an area, a centroid G(X_g,Y_g) can be defined using calculus by the equations,

X_g = (1/A)∫x.dA   ------ (i)

Where dA = elemental area and A= total area.

Y_g = (1/A)∫y.dA   ------ (ii)

HOW TO DERIVE THE VALUES OF X_g and Y_g FOR BASIC GEOMETRIC FIGURE:

STEPS TO FIND X_g


i) Draw the figure in a Coordinate System.

ii) Draw a thin strip of area of thickness (dx) parallel to Y axis and at a distance (x) from Y axis.

iii) Find the height of the strip. Either the height will be constant or the height is a function of (x), that can be calculated from the equation of the figure.

iv) Calculate the elemental area of the strip, and named as dA. Hence, dA = hdx

v) integrate the expression ∫xdA, but dA = hdx. Therefore, we shall integrate  ∫hxdx over the total area.

vi) X_g = (∫ xdA)/A = (∫ hxdx)/A ; where A = total area = ∫dA = ∫hdx


STEPS TO FIND Yg

i) Draw the figure in a Coordinate System.

ii) Draw a thin strip of area of thickness (dy) parallel to X axis and at a distance (y) from X axis.

iii) Find the length (b) of the strip. Either the length will be constant or the length is a function of (y), that can be calculated from the equation of the figure.

iv) Calculate the elemental area of the strip, and named as dA. Hence, dA = bdy

v) integrate the expression ∫ydA, but dA = bdy. Therefore, we shall integrate ∫bydy over the total area.

vi) Y_g = (∫ ydA)/A = (∫bydy)/A





CENTROID OF A COMPOSITE AREA:




HOW TO FIND THE CENTROID OF A COMPOSITE AREA

(a composite area consists of several straight or curved lines.)

(i) Draw the figure in a coordinate system. Draw the dimensions too. Every dimensions will be measured with respect to origin of the coordinate system

(ii) Divide the composite area into several parts of basic geometric areas. Lebel them as part-1, part-2, part-3, .......part-n. Let the corresponding areas are A₁, A₂, A₃, .... A_n. Let the centroids are G₁(X₁,Y₁), G₂(X₂,Y₂), G₃(X₃,Y₃), ...... G_n(X_n,Y_n).

(iii) Let the centroid of the composite area be G(Xg,Yg). Hence,
Xg = (A₁X₁ + A₂X₂ +A₃X₃)/(A₁ + A₂ + A₃)

Yg = (A₁Y₁ + A₂Y₂ +A₃Y₃)/(A₁ + A₂ + A₃)

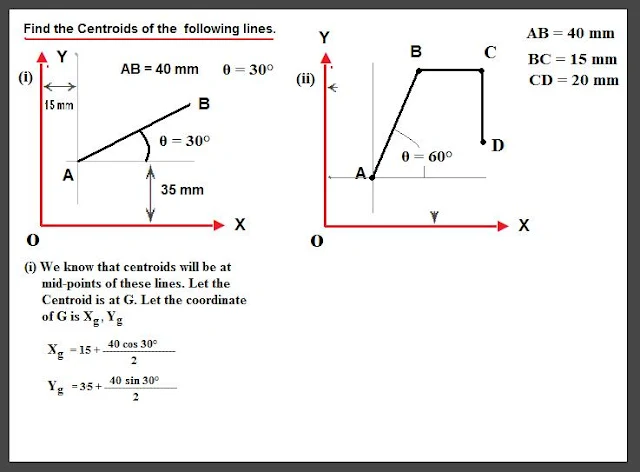
(a) Suppose we have certain area of magnitude (A) in a coordinate system. The centroid of the area will be at its mid-point. A centroid is denoted by G.
 
                       In the figure we have a complex geometrical area composed of three basic geometrical areas. A rectangle, a semi circle and a isosceles triangle. Let us denote the centroids as G₁, G₂, G₃ for the given areas in the figure.

We shall have to find the Centroid of the entire area composed of  A₁, A₂, A₃. 

At first, the composite line is divided into three parts.

Part -1 : The semi-circle : Let the centroid of the area A₁ be G₁(X₁,Y₁)

Area, A₁ = (π/2)x(25)² mm² = 981.74 mm²                  
          X₁ = { 25 -  (4x25)/(3xπ)} mm = 14.39 mm
          Y₁ = 25 mm

Part -2 : The Rectangle : Let the centroid of the A₂ be G₂(X₂,Y₂)

Area, A₂ = 100 x 50  mm² = 5000 mm²                 
          X₂ = 25 + (100/2) = 75 mm
          Y₂ = 25 mm
Part -3 : The Triangle : Let the centroid of the area Area, A₃ be G₃(X₃,Y₃)

Area, A₃ = (1/2) x 50 x 50 mm² = 1250 mm²                 
          X₃ = 25 + 50 + 25 = 100 mm
          Y₃ = 50 + (50/3) =  66.67 mm



If the centroid of the composite line be G  (X_g,Y_g)

X_g = (∑A_iX_i)/(∑A_i) 

    = (A₁X₁ + A₂X₂ +A₃X₃)/(A₁ + A₂ + A₃)
    = (981.74 x 14.39 + 5000 x 75 + 1250 x 100)/( 981.74 + 5000 + 1250)
    = 71.09
     

Y_g = (∑A_iY_i)/(∑A_i) 

    = (A₁Y₁ + A₂Y₂ +A₃Y₃)/(A₁ + A₂ + A₃)
    = (981.74 x 25 + 5000 x 25 + 1250 x 66.67)/ ( 981.74 + 5000 + 1250)
    = 32.20

Engineering Mechanics :: Equilibrium of a Particle Assignment No. 02

 Q1)  Two blocks of masses B and D are suspended as shown in the figure. The mass of B is 10 kg and the length of the chord is 4 m. If the g= 10 m/s2 , find the tension in the string and the reaction at the joints A and C.

ENGINEERING MECHANICS: GEOMETRICAL ANALYSIS Assignment No. : 01

1.	Solve the following equation for the two roots of x:   x2 — 16 = 0
	A. x = 2i,   –2i B. x = 4i,   –4i C. x = 4,   –4 D. x = 2,   –2

---

2.	Using the basic trigonomic functions, determine the length of side AB of the right triangle.
	A. h = 7.07 B. h = 10 C. h = 5 D. h = 14.14

---

3.	Determine the angle :
	A. = 30° B. = 40° C. = 60° D. = 50°

---

4.	Solve the following equation for x, y, and z: x – y + z = –1   –x + y + z = –1   x + 2y – 2z = 5
	A. x = 1,      y = 1,      z = –1 B. x = 5/3,      y = 7/6,      z = –1/2 C. x = –2/3,      y = –2/3,      z = –1 D. x = –1,      y = 1,      z = 1

---

5.	Using the basic trigonomic functions, determine the length of side AB of the right triangle.
	A. h = 5.77 B. h = 11.55 C. h = 5 D. h = 8.66

6.	Determine the angles and and the length of side AB of the triangle. Note that there are two possible answers to this question and we have provided only one of them as an answer.
	A. = 46.7°,  = 93.3° d = 9.22 B. = 50.0°,  = 90.0° d = 9.14 C. = 40.0°,  = 100.0° d = 9.22 D. = 48.6°,  = 91.4°, d = 9.33

---

7.	Determine the length of side AB if right angle ABC is similar to right angle A'B'C':
	A. AB = 5.42 B. AB = 3 C. AB = 5 D. AB = 4

---

8.	Determine the angle :
	A. = 30° B. = 40° C. = 60° D. = 50°

---

9.	Solve the following equation for the two roots of x:   — x2 + 5x = — 6
	A. x = 2,   3 B. x = –1,   –5 C. x = –1,   6 D. x = –0.742,   6.74

---

10.	Using the basic trigonomic functions, determine the length of side AB of the right triangle.
	A. h = 10 B. h = 7.07 C. h = 14.14 D. h = 5

CENTROID OF A STRAIGHT & CURVED LINE: ©subhankar karmakar 2011

CENTROID OF A STRAIGHT LINE:

(a) Suppose we have straight lines of length (L) in a coordinate system.  Let the lines are named as AB, BC and CA as shown in the figure. The centroids of these lines will at their mid-points viz. G₁, G₂, G₃.  The lines may be vertical, horizontal or inclined.

(b) For a curved line, a centroid G(X_g,Y_g)can be defined by the equations,

X_g = (1/L)∫x.dL   ------ (i)

Where dL = elemental length and L= total length of the line.

Y_g = (1/L)∫y.dL   ------ (ii)

Suppose we have a quarter circular arc in a co-ordinate system as shown in the figure. Total length of the arc AB = (πR)/2 . We take an arbitrarily small length of the arc CD and denote it as dL.

So, dL = Rdθ  ------ (iii)    [ as s=Rθ ]

Where R = Radius of the quarter circular arc. Let the co-ordinate of the point D be D(x,y) where   
x = Rcosθ -----(iv) and y = Rsinθ -----(v)

Hence   X_g = (1/L)∫x.dL  ;  

here L = (πR)/2

        x = Rcosθ 

     dL = Rdθ

     X_g = (2/πR)   ₀∫^π/2Rcosθ.Rdθ  =>  X_g = (2/πR) R²  ₀∫^π/2cosθ.dθ = 2R/π
      _Yg = (2/πR)   ₀∫^π/2Rsinθ.Rdθ  =>  _Yg = (2/πR) R²  ₀∫^π/2sinθ.dθ = 2R/π


                                                                           

                                                                                      
Hence, for a quarter circular arc of radius R will be G(2R/π,2R/π)


CENTROID OF A LINE CONSISTS OF SEVERAL SIMPLE LINES :

TRUSS ANALYSIS: THEORY OF TRUSS:

TRUSS ANALYSIS: THEORY OF TRUSS:

TRUSS :

Truss is a kind of framed structure made of entirely by rigid metallic rods joined by pin. The rods are called as Links or Linkages and the pins are called as joints. Their primary goal is to support the applied loads or we can say they are primarily load bearing structures. We often encounter trusses in our daily life as trusses are used to support roofs of various kinds of industrial sheds. Trusses are used as poles carrying high tension electricity.

LINK/ LINKAGES :

A link is a rigid rod which can bear any external load applied on it. A link can bear two types of forces.

COMPRESSIVE FORCES :

When the external forces applied on the link or rod tries to decrease the length of the rod, then they are called as External Compressive Forces. A truss in equilibrium counters this compressive force by inducing an internal force, equal and opposite the externally applied force. The internal force thus induced balancing the external compressive force is named as Internal Compressive Forces. Generally Compressive Forces are considered as negative in truss analysis.

TENSILE FORCES :

When external loads applied on a link try to increase the length of the link, we call them External Tensile Loads. To neutral the tensile load applied on a link, an equal but opposite internal force is generated named as Internal Tensile forces. Tensile forces are generally considered as positive internal forces.

THE SIMPLEST TRUSS:

A triangular shaped truss made of three linkages and three joints is the simplest type of truss. As it is the simplest geometric shape where there is no change in shape with the application of forces at the joints if the length of rods/ linkages remain unchanged / constant.

MAXWELL'S TRUSS EQUATION:

To distinguish between "statically determinate structure" and "statically indeterminate structure" Maxwell formulated an equation involving the number of linkages (m) and number of joints (j).

The trusses which satisfies the equation,
m = 2j - 3
are statically determinate structures and named as "Perfect Trusses".

If m > 2j - 3, then the number of linkages are more than required, hence, called as "Redundant Trusses".

Where as if m < 2j - 3 for any truss, then the number of linkages are less than that of a perfect truss. These kinds of trusses are called as "Deficient Trusses".



ASSUMPTIONS CONSIDERED WHILE ANALYZING TRUSSES :

While analyzing trusses, to simplify the analysis we often consider certain assumptions. The purpose of these assumptions are the simplification of a complex problems. The assumptions are

(i) The links are perfectly rigid bodies, ie there occurs no change in the dimensions of the links.

(ii) The pin joints are perfectly smooth, ie there is no friction in the each and every joints.

(iii) The mass and weights of the links are so small compare to the magnitudes of the applied forces, that for truss analysis we shall neglect them. It means the links are massless as well as weightless.

(iv) The cross-sections and material of the links are uniform by nature.

(v) The external loads are only applied on a joint in the truss, whenever we shall place any external load, we must place it one of the joints in the truss.

(vi) Stress in each member is constant along its length.

The objective of analyzing the trusses is to determine the reactions and member forces. The methods used for carrying out the truss analysis with the equations of equilibrium and by considering only parts of the structure through analyzing its free body diagram to solve the unknowns.

Method of Joints

 

 

The first to analyze a truss by assuming all members are in tension reaction. A tension member is when a member experiences pull forces at both ends of the bar and usually denoted as positive (+ve) sign. When a member experiencing a push force at both ends, then the bar was said to be in compression mode and designated as negative (-ve) sign.
In the joints method, a virtual cut is made around a joint and the cut portion is isolated as a Free Body Diagram (FBD). Using the equilibrium equations of ∑ F_x = 0 and ∑ F_y = 0, the unknown member forces could be solve. It is assumed that all members are joined together in the form of an ideal pin, and that all forces are in tension (+ve) of reactions.
An imaginary section may be completely passed around a joint in the truss. The joint has become a free body in equilibrium under the forces applied to it. The equations ∑ H = 0 and ∑ V = 0 may be applied to the joint to determine the unknown forces in members meeting there. It is evident that no more than two unknowns can be determined at a joint with these two equations.
 
Figure 1: A simple truss model supported by pinned and roller support at its end. Each triangle has the same length, L and it is equilateral where degree of angle, θ is 60° on every angle. The support reactions, R_a and R_c can be determine by taking a point of moment either at point A or point C, whereas H_a = 0 (no other horizontal force).
Here are some simple guidelines for this method of truss analysis:

1. Firstly draw the Free Body Diagram (FBD),
2. Solve the reactions of the given structure,
3. Select a joint with a minimum number of unknown (not more than 2) and analyze it with ∑ F_x = 0 and ∑ F_y = 0,
4. Proceed to the rest of the joints and again concentrating on joints that have very minimal of unknowns,
5. Check member forces at unused joints with ∑ F_x = 0 and ∑ F_y = 0,
6. Tabulate the member forces whether it is in tension (+ve) or compression (-ve) reaction.

 
Figure 2: The figure showing 3 selected joints, at B, C, and E. The forces in each member can be determine from any joint or point. The best way to start by selecting the easiest joint like joint C where the reaction R_c is already obtained and with only 2 unknown, forces of F_CB and F_CD. Both can be evaluate with ∑ F_x = 0 and ∑ F_y = 0 rules. At joint E, there are 3 unknown, forces of F_EA, F_EB and F_ED, which may lead to more complex solution compare to 2 unknown values. For checking purposes, joint B is selected to shown that the equation of ∑ F_x is equal to ∑ F_y which leads to zero value, ∑ F_x = ∑ F_y = 0. Each value of the member’s condition should be indicate clearly as whether it is in tension (+ve) or in compression (-ve) state.

* (Trigonometric Functions:
Taking an angle between member x and z…

• Cos θ = x / z
• Sin θ = y / z
• Tan θ = y / x )

Method of Sections

 

 

The section method is an effective method when the forces in all members of a truss are being able to determine. Often we need to know the force in just one member with greatest force in it, and the method of section will yield the force in that particular member without the labor of working out the rest of the forces within the truss analysis.
If only a few member forces of a truss are needed, the quickest way to find these forces is by the method of sections. In this method, an imaginary cutting line called a section is drawn through a stable and determinate truss. Thus, a section subdivides the truss into two separate parts. Since the entire truss is in equilibrium, any part of it must also be in equilibrium. Either of the two parts of the truss can be considered and the three equations of equilibrium ∑ F_x = 0, ∑ F_y = 0, and ∑ M = 0 can be applied to solve for member forces.
 

Figure 3: Using the same model of simple truss, the details would be the same as previous figure with 2 different supports profile. Unlike the joint method, here we only interested in finding the value of forces for member BC, EC, and ED.
Few simple guidelines of section truss analysis:

1. Pass a section through a maximum of 3 members of the truss, 1 of which is the desired member where it is dividing the truss into 2 completely separate parts,
2. At 1 part of the truss, take moments about the point (at a joint) where the 2 members intersect and solve for the member force, using ∑ M = 0,
3. Solve the other 2 unknowns by using the equilibrium equation for forces, using ∑ F_x = 0 and ∑ F_y = 0.

Note: The 3 forces cannot be concurrent, or else it cannot be solve.



 

Figure 4: A virtual cut is introduce through the only required members which is along member BC, EC, and ED. Firstly, the support reactions of R_a and R_d should be determine. Again a good judgment is require to solve this problem where the easiest part would be consider either on the left hand side or the right hand side. Taking moment at joint E (virtual pint) on clockwise for the whole RHS part would be much easier compare to joint C (the LHS part). Then, either joint D or C can be consider as point of moment, or else using the joint method to find the member forces for F_CB, F_CE, and F_DE. Note: Each value of the member’s condition should be indicate clearly as whether it is in tension (+ve) or in compression (-ve) state.

THE CONCEPT OF MOMENT:

Moment of force (or moment) is the tendency of a force to twist or rotate an object. This is an important, basic concept in engineering and physics. A moment is valued mathematically as the product of the force and the moment arm. The moment arm is the perpendicular distance from the point of rotation, to the line of action of the force. The moment may be thought of as a measure of the tendency of the force to cause rotation about an imaginary axis through a point. (Note: In mechanical and civil engineering, "moment" and "torque" have different meanings, while in physics they are synonyms.)


The moment of a force can be calculated about any point and not just the points in which the line of action of the force is perpendicular. Image A shows the components, the force F, and the moment arm, x when they are perpendicular to one another. When the force is not perpendicular to the point of interest, such as Point O in Images B and C, the magnitude of the Moment, M of a vector F about the point O is

where

is the vector from point O to the position where quantity F is applied.

× represents the cross product of the vectors.

[In the figure a moment at Point O, when the components are perpendicular to the Point O. Image B and Image C illustrate the components of a Moment at Point O, when the components are not perpendicular to point O.]

In mechanical engineering (unlike physics), the terms "torque" and "moment" are not interchangeable. "Moment" is the general term for the tendency of one or more applied forces to rotate an object about an axis (the concept which in physics is called torque). "Torque" is a special case of this: If the applied force vectors add to zero (i.e., their "resultant" is zero), then the forces are called a "couple" and their moment is called a "torque".
For example, a rotational force down a shaft, such as a turning screw-driver, forms a couple, so the resulting moment is called a "torque". By contrast, a lateral force on a beam produces a moment (called a bending moment), but since the net force is nonzero, this bending moment is not called a "torque".

A particle is located at position r relative to its axis of rotation. When a force F is applied to the particle, only the perpendicular component F⊥ produces a torque. This torque τ = r × F has magnitude τ = |r|  |F⊥| = |r| |F| sinθ and is directed outward from the page.

A Couple is a system of forces with a resultant (a.k.a. net, or sum) moment but no resultant force. Another term for a couple is a pure moment. Its effect is to create rotation without translation, or more generally without any acceleration of the centre of mass.

The resultant moment of a couple is called a torque. This is not to be confused with the term torque as it is used in physics, where it is merely a synonym of moment. Instead, torque is a special case of moment. Torque has special properties that moment does not have, in particular the property of being independent of reference point.

Simple Couple:

The simplest kind of couple consists of two equal and opposite forces whose lines of action do not coincide. This is called a "simple couple". The forces have a turning effect or moment called a torque about an axis which is normal to the plane of the forces. The SI unit for the torque of the couple is newton metre.
If the two forces are F and −F, then the magnitude of the torque is given by the following formula:

where

τ is the torque

F is the magnitude of one of the forces

d is the perpendicular distance between the forces, sometimes called the arm of the couple

The magnitude of the torque is always equal to Fd, with the direction of the torque given by the unit vector , which is perpendicular to the plane containing the two forces. When d is taken as a vector between the points of action of the forces, then the couple is the cross product of d and F.

  
Independence of reference point:

The moment of a force is only defined with respect to a certain point P (it is said to be the "moment about P"), and in general when P is changed, the moment changes. However, the moment (torque) of a couple is independent of the reference point P: Any point will give the same moment.In other words, a torque vector, unlike any other moment vector, is a "free vector". (This fact is called Varignon's Second Moment Theorem.)









The proof of this claim is as follows: Suppose there are a set of force vectors F₁, F₂, etc. that form a couple, with position vectors (about some origin P) r₁, r₂, etc., respectively. The moment about P is

Now we pick a new reference point P' that differs from P by the vector r. The new moment is

Now the distributive property of the cross product implies

However, the definition of a force couple means that

Therefore,

This proves that the moment is independent of reference point, which is proof that a couple is a free vector.