S.F.D. for CANTILEVER BEAMS

SHEAR FORCE DIAGRAMS OF THREE DIFFERENT TYPES OF CANTILEVER LOADING

CANTILEVER BEAM

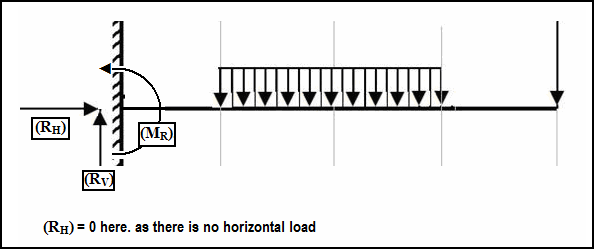
This is the most common beam in our surroundings. It is supported at one end with Fixed Joint and is known as Fixed End. The other end remains without any support and known as Free End. At the fixed end, there are a vertical reaction (R_V), a horizontal reaction (R_H) and a reaction moment (M_R).

How To Draw the Shear Force Diagram of a Cantilever.

(i) replace the fixed joint by a vertical, a horizontal reaction force and a reaction moment.

(ii) then divide the beam into different segment depending upon the position of the loads on the beam.

(iii) take the left most segment of the beam and draw a movable section within the segment.

(iv) let the distance of the extreme left end of the beam from the movable section line be X

(v) let the upward (vertical) forces or reactions are positive and the downward forces are negative. Now the sum of the total vertical forces left to the section line is equal to the shear force at the section line at a distance X from the left most end of the beam.

(vi) as positive SF produces positive Bending Moment, hence if we multiply all the forces those are in the left side of the section line with the distances of each force from the section line added with concentrated moment (clockwise as +ve, anti-clockwise as -ve) we get bending moment. So the sum of the products of each force that is in the left side of the section with the distance of it from section line added with pure moment on this section is equal to the Bending Moment at the section line.

CANTI-LEVER BEAM

 

Draw shear force & bending moment diagrams and equations

 

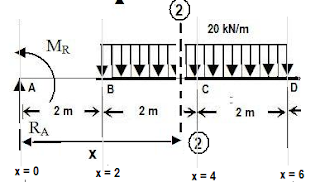
Solution: At first we shall find the reaction of the canti-lever beam.

A canti-lever beam is a common type of beam which is supported on a single fixed joint at one end. A fixed joint can provide a horizontal reaction, a vertical reaction and a reaction moment. While finding reaction we should transform a distributive load (UDL, UVL) to their equivalent concentrated or point load. An equivalent load of a distributed load can be found by placing the total load at the centroid of the distributed load diagram.  

FREE BODY DIAGRAM (FBD) OF THE BEAM

SF and BM Equations:

 Section AB (0 ≤ X≤ 2)

SF = R_A = 130 kN

BM = ‒ M_R + R_AX = ‒ 720 + 130X kN.m

At X = 0; SF = 130 kN and BM = ‒ 720 kN.m

At X =2; SF = 130 kN and BM = ‒ 720 + 260 = ‒ 460 kN.m

Section BD (2≤ X≤ 6)

SF = R_A ‒  20(X‒2) = 130  ‒  20(X‒2)

BM = ‒ M_R + R_AX  ‒  {20(X‒2)²}/2

= ‒ 720 + 130X ‒  {20(X‒2)²}/2

 At X = 2;  SF = 130 kN and BM = ‒ 460 kN.m

At X = 6; SF = 130 ‒  80 = 50 kN and BM = ‒ 720 + 780 ‒ 160 = ‒ 100 kN.m

When a distributive load remains fully on the left side of the section line as it is in the above diagram, we should use an equivalent point load in the place of Distributive load of UVL and UDL.

Section DE (6≤ X≤ 8)

SF = R_A ‒  80 = 130  ‒  80 = 50 kN

BM = ‒ M_R + R_AX  ‒  80(X ‒ 4) = ‒ 720 + 130X ‒  80(X ‒ 4)

At X = 6; SF = 130 ‒  80 = 50 kN and BM = ‒ 720 + 780 ‒ 160 = ‒ 100 kN.m

At X = 8; SF = 130 ‒  80 = 50 kN and BM = ‒ 720 + 1040 ‒ 320 = 0 kN.m

SFD and BMD