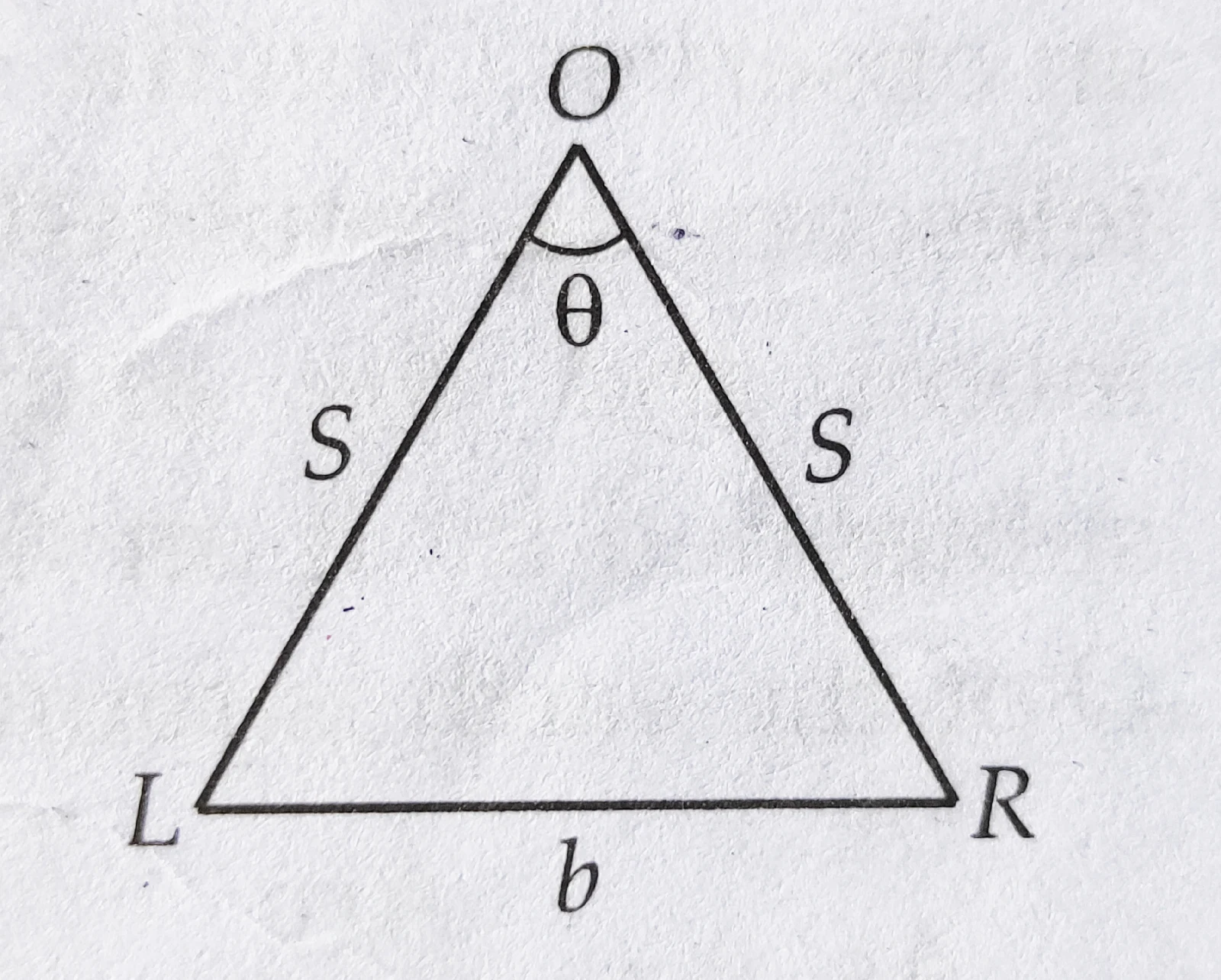LECTURE -3 : CLASS VIII : SCIENCE : CHAPTER 8 : CELLS, TISSUES, ORGANS, ORGAN SYSTEMS AND ORGANISM

CLASS VIII   |    SCIENCE    |    CHAPTER 8

      notes prepared by subhankar Karmakar

                                                                                  

1. CELLS: 

A cell is the smallest unit of life which has a definite structure and performs a specific function. 

All the cells of a multicellular organism are not similar. They are of many different shapes and sizes. Most of the cells are specialised to perform particular functions. They are called specialised cells. For example, in animals, muscle cells are specialised to contract and relax so that they can bring about movement in body parts. In plants, photosynthetic cells are specialised to carry out photosynthesis and make food. There are many types of specialised cells in animals and plants which perform different functions.

2. TISSUES:

The group of similar cells which work together to perform a particular function is called a tissue. For example, in animals, muscle tissue specialised to contract and relax so as to move body parts. Therefore, muscle tissue brings about movement in the body parts of animals. In plants, photosynthetic tissue is a group of photosynthetic cells joined together which is specialised to do photosynthesis and make food. There are many different types of tissues in both, animals as well as in plants. 

3. ORGANS:

An organ is a collection of different tissues which work together to perform a particular function in the body of an organism.

The multicellular organisms are made up of different organs which do different jobs for the organism. Some of the organs in animals are: 

Heart, Stomach, Brain, Lungs, Kidney, etc.

Some of the organs in plants are:

Roots, Stem, Leaf, Flower etc.

Each organ does different specialised work. 

Like in animals, 

a. The function of heart is to pump blood around the body.

b. The function of brain is to control all the parts of the body.

c. The function of lungs is to take in oxygen and give out carbon dioxide.

d. The function of the stomach is to digest the food.

In plants, 

a. The function of the roots is to absorb water and dissolve mineral salts from the soil.

b. The function of stem is to carry water and minerals from the roots to the leaves and the prepared food from the leaves to other parts of the plant.

c. The function of a leaf is to prepare food for the plant by the process of photosynthesis.

d. The flowers are reproductive organs which led to the formation of fruits and seeds. The fruit protects the seeds.

4. ORGAN SYSTEMS:

A group of interconnected organs which works together to do a big job for the organism, is called an organ system. 

All the multicellular animals and plants have many organ systems in their bodies to carry out various life processes. 

For example, the various organ systems of animals are:

Digestive system, respiratory system, circulatory system, nervous system, excretory system, reproductive system, muscular system and skeletal system. 

The plants have two main organ systems:

Root system and shoot system.

Work of the organ systems:

The function of digestive system is to break down the food into simple substances which can be absorbed by the body. The main organs of the digestive system are:

Mouth, Oesophagus, stomach, small intestine, large intestine, rectum and anus. 

5. ORGANISM:

An organism is an animal or a plant which can exist on its own. An organism is made up of many different organ systems which work together to perform all the functions necessary for maintaining life.

Multicellular organisms are built like in the following sequence. 

1. Cells make up tissues

2. Tissues make up organs

3. Organs make up organ systems

4. Organ systems makeup an organism

LECTURE: 1 : CLASS XI: PHYSICS : UNITS & MEASUREMENTS

CLASS XI   |    PHYSICS    |    CHAPTER 2

      notes prepared by subhankar Karmakar

PHYSICAL QUANTITIES:

All those quantities which can be measured directly or indirectly and in terms of which the laws of Physics can be expressed are called physical quantities. For example, length, mass, time, speed, temperature, force, electric current, angle etc are physical quantities.

TYPES OF PHYSICAL QUANTITIES:

Physical quantities are of two types:

a. Fundamental quantities

b. Derived quantities

a. FUNDAMENTAL QUANTITIES:

The physical quantities which can be treated as independent of other physical quantities and are not usually defined in terms of other physical quantities are call fundamental quantities. There are seven fundamental quantities, and two supplementary fundamental quantities.

The fundamental or base quantities are:

1. Mass

2. Length

3. Time

4. Electric current

5. Thermodynamic temperature

6. Luminous intensity

7. Amount of substance

Two supplementary fundamental quantities are:

1. Angle

2. Solid angle

b. DERIVED QUANTITIES:

The physical quantities who's defining operations are based on other physical quantities are called derived quantities. All physical quantities other than fundamental quantities are derived quantities. For example, velocity, speed, acceleration, force, momentum etc are derived quantities.

THE MEASURING PROCESS:

Measurement: The measurement of a physical quantity is the process of comparing this quantity with a standard amount of the physical quantity of the same kind, called its unit. 

The measurement of a physical quantity has two components.

1. The unit in which the quantity is measured (u)

2. The numerical value or the magnitude of the quantity. (n)

If the measure of a physical quantity = Q

Numerical value of the physical quantity = n

Size of the unit = u, then

Q = nu

If n₁ and n₂ are the numerical values for a physical quantity Q corresponding to the units u₁ and u₂ , then

Q = n₁u₁ =  n₂ u₂

PHYSICAL UNIT:

The standard amount of a physical quantity chosen to measure the physical quantity of the same kind is called a physical unit.

Desirable characteristics of a physical unit:

1. It should be well defined.

2. It should be of convenient size. Neither too small, nor too large.

3. It should not change with time.

4. It should be easily reproducible.

5. It should be imperishable or indestructible.

6. It should not be affected by the change in physical conditions such as variation of pressure temperature etc.

7. It should be internationally acceptable.

8. It should be easily accessible.

FUNDAMENTAL & DERIVED UNITS:

Fundamental units: The physical units which can neither be derived from one another, nor they can be further resolved into more simpler units are called fundamental units. Units of fundamental quantities are fundamental units.

Derived units: All the other physical units which can be expressed in terms of the fundamental units are call derived units. Like unit of force is Newton, but it can be expressed in terms of fundamental units.

Force = Mass x acceleration

1 N = 1 kg x 1 m /s² = 1 kg m /s²

DIFFERENT SYSTEM OF UNITS:

a. cgs system = It was set up in France. It is based on centimetre, gram and second as the fundamental units of length, mass and time respectively.

b. mks system = It is also a French system based on metre, kilogram and second as the fundamental units of length, mass and time respectively.

c. SI system = It is the international system of units. What is the modernization extended form of the mks system. 

BASIC SI QUANTITIES AND UNITS:

Basic quantity - basic unit - symbol

1. Length - metre - m

2. Mass - kilogram - kg

3. Time - second - s

4. Temperature - kelvin - K

5. Electric Current - ampere - A

6. Luminous Intensity - candela - cd

7. Quantity of matter - mole - mol

Supplementary units

1. Angle - radian - rad

2. Solid angle - steradian - sr

Definition of Radian and Steradian:

1. Radian: it is defined as the plane angle subtended at the centre of a circle by an Arc equal in length to the radius of the circle.

θ (in radians) = arc/radius = l/r

2. Steradian: it is defined as the solid angle subtended at the centre of a sphere why the surface of the sphere equal in area to that of a square having each side equal to the radius of the sphere. 

Ω (in steradian) = surface area/ radius²

Some common practical units:

1. Fermi = it is also known as femtometre. It is a very small unit of distance. It is used to measure nuclear distance. The radius of a proton is 1.2 fermi.

1 fermi = 10⁻¹⁵ m

2. Angstrom (Å): 

It is also a small unit of distance. It is used express wavelength of light.

1 Å = 10⁻¹⁰ m = 10⁻⁸ cm

3. Nano-metre:

It is also used to express wavelength of light.

1 nano metre = 10⁻⁹ m

4. Micron (μm)

It is also known as micro metre. 

1 μm = 10⁻⁶ m

5. Astronomical Unit ( AU)

It is defined as the the mean distance of the earth from the sun. It is a practical unit used for measuring large distances. It is used in astronomy to measure distances of planets.

1 AU = 1.496 x 10¹¹ m

6. Light year (ly)

It is the distance travelled by light in vacuum in one year. Light year is used in astronomy to measure distances of nearby stars. Like alpha centauri, the nearest are outside the solar system is 4.3 light years away from the Earth.

1 ly = 9.467 x 10¹⁵ m

7. Parsec or Parallactic Second:

It is the largest practical unit of distance used in astronomy. It is defined as the distance, at which an Arc of length 1 astronomical unit subtends an angle of 1 second of arc. 

1 parsec = 3.26 ly = 3.08 x 10¹⁶ m

Indirect method for measuring large distances:

a. Triangulation method for the height of an inaccessible object.

b. Parallax method to measure the distance of a nearby star. 

* Sextant: sextant is an instrument by which we can measure the angle of a distant object with the horizontal.

a. Triangulation method for the height of an inaccessible object.

Let AB = h be the height of the mountain to be measured. By using a sextant, we first measure the angle of elevation of its peak from my point C on the ground. Let it be θ₁ or ∠ACB  =  θ₁  . Move the sextant to another position D such that CD = d. Again measure the angle of elevation, ∠ADB = θ₂ . 

in right triangle ∆ABC, 

cot  θ₁ = CB/AB = x /h

in right triangle ∆ABD, 

cot  θ₂ = DB/AB = (d + x )/h

cot  θ₂ -  cot  θ₁ = (d + x )/h - x/h = d/h

∴ h = d / ( cot  θ₂ -  cot  θ₁ )

Hence, if we know d , the height h can be determined.

b. Parallax method

Parallax: parallax is the apparent shift in the position of an object with respect to another when we shift our eye side wise.

suppose we hold a pen O at a distance S from the eyes. Look at the pen first by the left eye L closing the right eye, and then buy the right eye R closing the left eye. The position of the  pen appears to change with respect to the background. This is called parallax. The distance between the two points of observation is called basis. In this case, the distance LR = b between the two eyes is the basis. ∠LOR = θ is called parallax angle or parallactic angle.

Parallax method can be used to find the

1. Distance of moon or any other planet.

2. Distance of a nearby star. 

1. Distance of moon or any other planet.

To measure the distance S of the moon or a faraway planet P, we observe it simultaneously from two different positions (observatories) A and B on the earth, separated by a large distance AB = b. We select a distant star S' whose position and direction can be taken approximately same from A and B. 

      Now, ∠PAS' = Φ₁ and ∠PBS' = Φ₂ are measured from the two observatories at the same time. As b<<S, so we can take AB as an arc of length b. 

      Now  θ = Arc/Radius = b/s

                      ∴ S = b/θ

where θ = ∠APB = Φ₁ + Φ₂ , is the parallactic angle. 

2. Distance of a nearby star. 

Suppose N is a nearby star whose distance d from the earth is to be found. F is a far off star whose direction and position is fixed for all the position of the earth in its orbital motion. When the earth is at position A, the parallax angle between distance star F and nearby star N is determined. Let it be θ₁ . After 6 months, the earth is at diametrically opposite position B. The parallax angle ∠NBF = θ₂ is measured. 

Total parallax angle subtended by N on the earth's orbital diameter AB is 

                θ = θ₁ +  θ₂

As,           θ = Arc/Radius

                θ = AB/d

             ∴ d = AB/θ

This Parallax method is useful for measuring distances of stars which are less than 100 light years away from the Earth. 

LECTURE -2 : CLASS VIII : SCIENCE : CHAPTER 8 : CELL STRUCTURE & FUNCTIONS

CLASS VIII   |    SCIENCE    |    CHAPTER 8

      notes prepared by subhankar Karmakar

Comparison of Plant Cells and Animal Cells:

* A General diagram of a plant cell

* A general diagram of an animal cell

The main similarities between plant cells and animal cells are given below:

1. Plant cells and animal cells have a cell membrane or plasma membrane around them.

2. Plant cells and animal cells have cytoplasm.

3. Plant cells and animal cells have a nucleus.

4. Plant cells and animal cells have a nuclear membrane.

5. Plant cells and animal cells have mitochondria.

The main differences between plant cells and animal cells are given below:

1. A plant cell has a cell wall around it, but an animal cell does not have a cell wall around it.

2. A photosynthetic plant cell has chloroplasts in it. Other plant cells have different plastids in them, but in an animal cell there is no chloroplasts or other plastids.

3. A plant cell has a large vacuole in it, but an animal cell usually does not have any vacuole, some animal cells have small vacuoles.

Prokaryotic cells and Eukaryotic cells:

a. Prokaryotic cells and prokaryotes:

The primitive cells, where nucleus of the cell is not properly organised and they do not have any nuclear membrane around the nuclear material and they are called prokaryotic cells. In prokaryotic cells, the nuclear material is in direct contact with the cytoplasm.

The organisms made of prokaryotic cells are called prokaryotes. 

 All the prokaryotes are simple, unicellular organisms. Most of the bacteria and blue green algae are prokaryotes. 

 b. Eukaryotic cells and Eukaryotes:

The cells having nuclear material enclosed by a nuclear membrane are called Eukaryotic cells. Eukaryotic cells have a proper, well organised nucleus and nucleus are separated from the cytoplasm by nuclear membrane. Eukaryotic cells are more advanced then prokaryotic cells. 

The organisms which are made of Eukaryotic cells are called Eukaryotes. All the organisms other than bacteria and blue green algae are Eukaryotes. For example, Amoeba is an Eukaryote. Eukaryotes may be unicellular or multicellular. 

Different organisms having variety in cell number, cell shape and cell size:

A. Variety in the number of cells:

Different organisms have different number of cells in their bodies.

B. Variety in shape of cells:

The cells in multicellular organisms have many different shapes.

C. Variety in size of cells:

The cells in multicellular organisms can have many different sizes.

A. Variety in the number of cells:

Depending on the number of the cells, in the body of an organism, an organism is called unicellular or multicellular. 

(i) Unicellular Organisms:

The organisms which are made up of only one cell are called unicellular organism. It is also known as single celled organism. Some of the examples of unicellular organisms are:

Amoeba, Paramecium, Euglena, Chlamydomonas and bacteria.

The single cell of all the unicellular organisms behaves as a complete organisms. A unicellular organism can perform all the necessary life functions with the help of just one cell. For example, Amoeba is a tiny animal which consists of only one cell but can perform all the basic functions of life like taking food, digestion, respiration, movement, response to environmental changes, removal of waste and reproduction etc. 

(ii) Multicellular Organisms:

The organisms which are made up of many cells are called multicellular organisms. Most of the plants and animals around us, including us are multicellular organisms. Multicellular organisms millions and billions of cells which vary in shapes and sizes. Different groups of cells perform a variety of functions. A multicellular organism starts its life as a single cell called fertilized egg cell or Zygote. 

B. Variety in shape of cells:

There are many types of cells in the bodies of multicellular organisms. These cells differ in shapes. For example, the shape of nerve cell in animals is very different from the shape of a muscle cell. A nerve cell is long and branched whereas a muscle cell is pointed at both ends and has a spindle shape and an epithelial cell is rectangular shape. Cells are different in shapes and sizes so that they can perform different functions. Some of the examples of animal cells which have different sizes and shapes are: nerve cell or neuron, muscle cell, epithelial cell, red blood cell, white blood cells, bone cell and cartilage cell. 

Different shape of a cell helps in its functioning. Like nerve cells are long and have projections so that they can make contacts with many other Nerve cells and carry messages over long distances like between brain and other parts of body. Muscle cells bring about the moment at body parts by contracting and relaxing, hence, they are pointed at the both ends and spindle shaped. 

Some of the important plant cells are: epidermal cells, xylem cells, phloem cells, and photosynthetic cells. The epidermal cells form a layer around the plant organs and protect the cells below from injury, xylem cells are the tube like plant cells having thick and strong walls which carry water and mineral salts from the roots of the plant to the leaves. Phloem cells are also tubelight plant cells having thin walls which carry the food made by leaves to all other parts of the plant. The photosynthetic cells of the plant contain chlorophyll and prepare food by photosynthesis. The mesophyll cells of leaf are the photosynthetic plant cells. These cells in the leaf of a plant are specially adapted for making food by photosynthesis. 

Amoeba: 

All the plant and animal cells are not capable of independent existence, the single celled organism like amoeba can exist independently. 

The shape of amoeba cell is irregular. In fact the Amoeba cell has no fixed shape. The 

Amoeba cell keeps on changing its shape continuously. Shape of Amoeba cell changes because amoeba can make its cytoplasm in any direction it wants to. The Amoeba cell finger like projections of varying lengths protruding out of his body which is called pseudopodia. 

Amoeba derives two advantages by changing shape: 

The changing of shape due to the formation of pseudopodia helps amoeba in 

1. movement

2. In capturing food.

C. Variety in size of cells:

The cells are of many different sizes. Some are so small that they cannot be seen with the naked eyes, whereas large cells also exists. Generally most of the cells are extremely small in size, like bacteria cells have a length of 0.1 micrometer ~ 0.5 micrometer. The smallest cell is bacteria mycoplasma, which is only 0.1 micrometre long. Whereas, the birds eggs are very large cells, they can be seen easily with naked eye. Each egg of the bird is a single cell, like the hen's egg is a single cell. The biggest cell is the ostrich egg which is approximately 17 cm long. The size of cells has no relation with the size of the body of an animal. Rather it is related to its function. 

LECTURE 1 : CLASS XI: PHYSICS : MOTION IN ONE DIMENSION

CLASS XI   |    PHYSICS    |    CHAPTER 3

      notes prepared by subhankar Karmakar

Rest : An object is said to be at rest if it does not change its position with respect to its surroundings with time.

Motion: An object is said to be in motion if it changes its position with respect to its surroundings with time.

Distance / path length: (s or x)

It is the length of the actual path travelled by a body between its initial and final positions. It is a scalar quantity.

The SI unit of distance is metre

The CGS unit of distance is centimetre

Displacement: (s or x)

The displacement of an object is the change in the position of an object in a fix direction. It is a vector quantity.

The SI unit of displacement is  metre 

The CGS unit of displacement is centimetre

Speed: (v)

The distance travelled per unit time is called speed. 

Speed = distance travelled/ time taken

         v = s/t

It is a scalar quantity

The SI unit of speed is m/s or ms⁻¹

The CGS unit of speed is cm/s or cms⁻¹

The dimensional formula of speed is [M⁰L¹T⁻¹]

Velocity: (v) 

The rate of change of position of an object which time in  a given direction is called its velocity.(v)

Velocity= displacement/time

It is a vector quantity.

SI unit of velocity is m/s

CGS unit of velocity is cm/s

The dimensional formula of velocity is [M⁰L¹T⁻¹]

Acceleration: 

The rate of change of velocity of an object with time is called its acceleration. (a)

Acceleration= change in velocity/time taken

It is a vector quantity.

The SI unit of acceleration is m/s²

The CGS unit of acceleration is cm/s²

The dimensional formula of acceleration is [M⁰L¹T⁻²]

Different types of speed

There are four types of speed

1. Uniform speed

2. Variable speed

3. Average speed

4. Instantaneous speed

Uniform speed: if a body covers equal distances in equal intervals of time the body is said to be in uniform speed.

Variable speed: if a body covers unequal distances in equal intervals of time the body is in variable speed.

Average speed: the ratio of Total distance travelled and total time taken is called average speed

Instantaneous speed: the speed of an object at any particular instant of time is called instantaneous speed of that object.

Different types of velocity:

There are basically four types of velocity

1. Uniform velocity

2. Variable velocity

3. Average velocity

4. Instantaneous velocity

Uniform velocity: a body is said to be moving with uniform velocity if it covers equal displacements in equal intervals of time.

Variable velocity: a body is said to be moving with variable velocity if either its speed changes or direction of motion changes or or both change with time

Average velocity: the ratio of total displacement and total time is called average velocity

Instantaneous velocity: the velocity of an object at a particular instant of time or at a particular point of its path is called its instantaneous velocity.

How to calculate average speed in different situations:

a. A body covering different distances with different speeds:

Suppose a body covers distances s₁, s₂, s₃.... with speeds v₁, v₂, v₃... respectively, then its average speed will be

vₐ = (s₁+ s₂ + s₃... )/(t₁ + t₂ + t₃... )

⟹ vₐ =  (s₁+ s₂ + s₃... )/(s₁/v₁ + s₂/v₂ +  s₃/v₃ .....)

(i) if s₁ = s₂ = s

vₐ =  (s₁+ s₂)/(s₁/v₁ + s₂/v₂)

⟹ vₐ = (s + s)/(s/v₁ + s/v₂)

⟹ vₐ = (2s)/s(1/v₁ + 1/v₂)

⟹ vₐ = (2v₁v₂)/(v₁ + v₂)

As an example suppose a body travels from A to B at 40 m/s and from B to A at 60 m/s. Calculate the average speed.

Soln. Here the distances of same ie.  s₁ = s₂ = s

As AB distance = BA distance

∴  vₐ = (2v₁v₂)/(v₁ + v₂)

    ⟹ vₐ = (2x40x60)/(40 + 60)

    ⟹ vₐ = (2x40x60)/100

    ⟹ vₐ = 48 m/s

b. A body moving with different speeds in different time intervals:

Suppose a body travels with speeds v₁, v₂, v₃, ...

In time intervals   t₁,  t₂,  t₃ .......

Respectively, then

Total distance travelled = v₁t₁ +  v₂t₂ + v₃t₃ + .....

Total time taken = t₁ + t₂ + t₃ + ........

∴  vₐ = (v₁t₁ +  v₂t₂ + v₃t₃ + .....)/( t₁ + t₂ + t₃ + ..)

As an example, if a body travels along a straight line for the first 10 minutes with speed 30 km/h, and the next 20 minutes with speed 60 km/h. Find the average speed of the body.

Soln. Here,  v₁ = 30 km/h; v₂ = 60 km /h

t₁ = 10 min = 10/60 h = 1/6 h

t₂ = 20 min = 20/60 h = 2/6 h

∴  t₁ + t₂ = 1/6 + 2/6 = 3/6 = 1/2 h

We know,  vₐ = (v₁t₁ +  v₂t₂)/( t₁ + t₂)

∴  vₐ = {30x(1/6)+60x(2/6)}/(1/2)

⟹ vₐ = (5 + 20)/(1/2)

⟹ vₐ = 25x2 = 50 km/h

CLASS XI: PHYSICS : CHAPTER-1 : PHYSICAL WORLD

CLASS XI   |    PHYSICS    |    CHAPTER 1

      notes prepared by subhankar Karmakar

Q1. What is scientific method? Mention the various steps involved in it.

Ans. Scientific method: the step-by-step approach used by a scientist in studying natural phenomena and establishing laws which govern these phenomena is called scientific method. 

Generally, it involves the following steps:

a. Taking a large number of systematic observations by doing controlled experiments.

b. Studying these observations and making qualitative and quantitative reasoning.

c. Suggesting mathematical models to account for the observed behaviour.

d. Predicting new phenomena on the basis of suggested model.

e. Modifying the theory, if necessary, the light of fresh evidences.

Q2. Name the four basic forces in nature. Arrange them in the order of their increasing strengths.

Ans. Fundamental forces in nature: 

In the macroscopic world, we observe several kinds of forces. All the forces between microscopic objects arise from two fundamental forces:

a. Gravitational force(F_g) 

b. Electromagnetic force. (F_e)

In the microscopic world, there are two more basic forces:

c. Strong nuclear force(F_s)

d. Weak nuclear force (F_w)

(F_g) : (F_w) : (F_e) : (F_s) = 1: 10²⁵ : 10³⁶ : 10³⁸

Q3. Describe briefly the fundamental forces in nature.

Ans. There are four fundamental forces in nature. They are as follows:

a. Gravitational force(F_g) 

b. Electromagnetic force. (F_e)

c. Strong nuclear force(F_s)

d. Weak nuclear force (F_w)

Gravitational force(F_g) : it is a force of mutual attraction between two bodies by virtue of their masses. According to the Newton's law of gravitation, the gravitational attraction between two bodies of masses m₁ and m₂ separated by a distance r is given by

   F_g = Gm₁m₂/r²

Where G is the universal gravitational constant.

Electromagnetic force (F_e): 

The force acting between two electric charges at rest is called electrostatic force. Electrostatic force is a part of electromagnetic force. According to Coulomb's law, the magnitude of the electrostatic force (F_e) between two point charges q₁ and q₂ separated by a distance r in vacuum is given by

(F_e) = (1/4πεₒ).q₁q₂ / r²

Where εₒ is the permittivity of vacuum. 

The force acting between two magnetic poles is called magnetic force.

Together electrostatic force and magnetic force is known as electromagnetic force.

Weak nuclear force (F_w):

It is a force that appears only between elementary particles involved in a nuclear process such as the β-decay of a nucleus.  It is a short range force that operates only over the size of a nucleus (= 10⁻¹⁵ m)

Strong nuclear force(F_s):

The strong attractive force which binds together the protons and neutrons in a nucleus is called strong nuclear force. It is a short range force that operates only over the size of a nucleus (= 10⁻¹⁵ m)

Q4. What are the different conservation laws in Physics?

Ans. Conservation laws: in any physical process involving the different forces, some physical quantities, remain unchanged with time. Such quantities are called conserved quantities. The laws which govern the conservation of these quantities are called conservation laws.

There are four basic conservation laws:

a. Law of conservation of energy.

b. Law of conservation of linear momentum

c. Law of conservation of angular momentum

d. Law of conservation of charge.

Q5. Name the scientist who was first awarded two Nobel prizes.

Ans. Madame Marie Curie , for physics ine 1903 and for chemistry in 1911.

Q6. Who first discovered radioactivity?

Ans. A H Becquerrel in 1896.

Q7. Mention some important contributions of Albert Einstein to physics.

Ans. a. Mass energy equivalence

         b. Photoelectric effect

         c. Special theory of relativity

         d. General theory of relativity.

Q8. Name the Indian physicist who was first awarded the Nobel prize.

Ans. C V Raman.

Q9. What was the important discovery of CV Raman?

Ans. Inelastic scattering of light by molecules.

Q10. What was the major contribution of Indian physicist SN Bose?

Ans. Quantum statistics ( Bose Einstein statistics)

Q11. With which field work was the famous Indian physicist H J bhabha associated?

Ans. Cascade process in cosmic radiation.

Q12. Name the Indian physicist associated with the triple helical structure of proteins.

Ans. G N Ramachandran.

CLASS XI: PHYSICS : MOTION IN ONE DIMENSION : NUMERICALS

CLASS XI  |    PHYSICS    |    CHAPTER 3

      notes prepared by subhankar Karmakar

Q.1. A car is moving with a velocity 54 km per hour. It suddenly applied brake and comes to rest within 0.6 s. How much distance it will travel before it comes to rest?

Q2. A body travels a distance s₁ with velocity v₁ and distance s₂ with velocity v₂ in the same direction. Prove that the average velocity of the body

vₐ = {(s₁ + s₂)v₁v₂}/(s₁v₂ +  s₂v₁)

Q3. A car travels along a straight line for the first half time which speed 50 km/h and the second half time with speed 60 km/h. Find the average speed of the car.

Q4. On a foggy day, two driver spot each other when they are just 80m apart. They are travelling at 72 km/h and 54 km/h respectively. Both of them applied brakes retarding their cars at the rate of 5 m.s⁻². Determine whether they never collision or not.

Q5. A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t second, then prove that

(i) the maximum velocity attained by the car

  Vₘₐₓ = (αβt)/(α + β)

(ii) the total distance travelled buy the car

  X  = (αβt²)/2(α + β)

Q6. A body covers 12 m in 2nd second and 20 m in 4th second. How much distance will it cover in 4 seconds after the 5th second?

Q7. Two buses A and B are at positions 50 m and 100 m from the origin at time t = 0. They start moving in the same direction simultaneously with uniform velocity of 10 m/s and 5 m/s. Determine the time and position at which A overtakes B. 

Q8.  A body covers a distance of 20 m in the 7th second and 24 m in the 9th second. How much shall it cover in 15th second?

Q9. An object is moving with uniform acceleration its velocity after 5 seconds is 25 m/s and after 8 seconds it is 34 m/s. Find the the distance travelled by the object in 12th second.

Q10. A ball thrown vertically upwards with a speed of 19.6 m/s from the top of a tower returns to the earth  in 6 second. Find the height of the tower. 

Q11. A ball is thrown vertically upwards with a velocity 20 m/s from the top of a multistoried building. The height of the point from where the ball is thrown is 25 m from the ground.

(a) How high will the ball rise? 

(b) How long will it be before the ball hits the ground?    (Take g = 10 m/s²)

Q12. Two balls are thrown simultaneously, A vertically upwards with a speed of 20 m/s from the ground, and B vertically downwards from a height of 40 m with the same speed and along the same line of motion. At what point do the two balls collide? 

LECTURE -1 : CLASS VIII : SCIENCE : CHAPTER 8 : CELL STRUCTURE & FUNCTIONS

CLASS VIII   |    SCIENCE    |    CHAPTER 8

      notes prepared by subhankar Karmakar

Cell : Cells are the basic units of life. All the living things both plants and animals, are made from cells. Cells are tiny basic unit of structure and function of all living organisms. Cells are the building blocks of plants and animals. Therefore, we can say a cell is the smallest unit of life which has a definite structure and performs specific function.

Microscope: The instrument used to study cells is called microscope.

Discovery of cell: an English scientist named Robert hooke discovered cell in 1665.

In 1838, a German scientist Schleiden first suggested that all plants are made of cells. 

In 1839, another German scientist Schwann suggested that all animals are made of cells too. 

Cell division: all cells arise from pre-existing cells by a method which is called cell division.

Classification of cell: All cells are primarily categorised into two main types. Animal cells and plant cells. 

Structures of a cell: Each cell has a number of smaller parts or internal structures in it. Some of the structures are present in both animal and plant cells, while some structures are only present in plant cells, they are not present in animal cells. They are also called parts of a cell.

The parts of a cell present in both animal and plant cells: 

Cell membrane or plasma membrane, Cytoplasm, Nucleus and Mitochondria. These basic parts are present in in both animal as well as plant cells. 

.                  Parts of a cell

The parts of a cells present in plant cells only:

Cell wall, Chloroplasts, Large vacuole are present in plant cell only. 

.               Parts of a Plant Cell

1. Cell membrane or plasma membrane:

Every cell is covered by a thin sheet of skin which is called cell membrane or plasma membrane. The cytoplasm and nucleus are enclosed within the cell membrane. Therefore we can say, cell membrane encloses the living part of the cell which is known as protoplasm. 

The cell membrane protects the cell and also gives shape to the cell. The cell membrane has tiny pores in it. Through this pores, the cell membrane controls the movement of substances "into the cell" and "out of the cell" like the dissolved glucose and oxygen can enter into the cell whereas the waste products like carbon dioxide can go out from the cell through this pores of the cell membrane. 

Cell membrane separates the cell from other cells as well as from the surrounding medium. The cell membrane or plasma membrane is a living part of the cell.

2. Cytoplasm: 

Cytoplasm is a transparent jelly like material which fills the cell between nucleus and the cell membrane. It acts like a chemical factory of the cell. In cytoplasm, new substances are built from materials taken into the cell and energy is released and stored. It is a place where most of the chemical reactions which keep the cell alive take place. Cytoplasm has many internal structures which are known as organelles. The most prominent internal structure in the cytoplasm is nucleus. It also contains mitochondria, Golgi bodies, ribosomes etc. Cytoplasm for plant cells also contain chloroplast. Cytoplasm and the nucleus taken together is called protoplasm.

3. Nucleus:

Nucleus is a large spherical organelle present in all the cells. In animal cell, nucleus lies in the centre of the cell whereas in plant cells the nucleus maybe on the periphery of the cell.  Nucleus is separated from the cytoplasm by a membrane called nuclear membrane. Nucleus controls all the activities of cell. The transmission of characteristics from the parents to the offsprings is called inheritance and Nucleus plays a role in inheritance.  

Chromosome: Nucleus contains thread like structure called chromosome. The function of chromosomes is to transfer the characteristics from the parents to the offspring through the genes and it is called inheritance. 

Nucleolus: The nucleus also contains a tiny round structure called nucleolus. The nucleus containing chromosomes and nucleolus is bound by a membrane called nuclear membrane. Nuclear membrane has tiny pores for the exchange of materials with cytoplasm. Some cells like red blood cells do not have a nucleus.

Gene: Gene is a unit of inheritance in living organisms, which is transferred from parent to offspring during reproduction and determine some characteristic feature of the offspring. Thus genes control the transfer of hereditary characteristics from parents to offsprings. 

Protoplasm: All the living matter in a cell is called protoplasm. Protoplasm is a liquid substance which is present inside the cell membrane. Protoplasm includes cytoplasm, nucleus and other organelles. Most of the protoplasm is made up of compounds of only 4 elements Carbon, Hydrogen, Nitrogen and Oxygen. It also contains water, carbohydrates, proteins, nucleic acids, fats and mineral salts.

4. Mitochondria: 

Mitochondria are the tiny rod-shaped or spherical organelles which are found in all the cells. Mitochondria provide energy for all the activities of the cell. This energy is produced by the process of respiration in which food such as glucose is broken down by oxygen. Thus mitochondria use glucose and oxygen to produce energy. Mitochondria are found in large numbers in the cytoplasm in all the cells.

5. Cell wall: The plant cells have a thick cell wall around them outside the cell membrane. The cell wall is made of a tough material called cellulose. Cell wall gives shape and support to the plant cell. Cell walls also hold the plant cells together and give plants most of their strength. Plants need protection against high wind speed, variation in temperature and atmospheric moisture etc. Since plants are fixed at a place so they cannot move to protect themselves from the various changes in their surroundings. The tough cell wall present in plant cells provides protection to plants. Cell wall is not there in animal cells. The cell wall is a non living part of the plant cells.

6. Chloroplasts: Chloroplasts are the green coloured organelles present in the cytoplasm of plant cells. The process of food making by plants known as photosynthesis takes place in chloroplasts. The green colour of chloroplasts is due to the presence of a green pigment called chlorophyll in them. Chlorophyll can absorb sunlight energy. In the chloroplasts, carbon dioxide and water combine in the presence of sunlight energy to produce food such as glucose. And this process of food making is called photosynthesis. 

The organelles containing pigments or colour matter present in the cytoplasm of plant cells are called plastids. Plastids can be of many different colours. The plastids containing green pigment or chlorophyll are known as chloroplasts. Chloroplast are present in the cells of leaves. It makes the leaves green. The plastids are may be of different colour like red colours of tomatoes are due to red plastids. Different colours of flowers are also due to this plastids.

7. Large Vacoule: 

Vacoule is a space in the cytoplasm of a cell which is enclosed by a membrane and is usually contains substances dissolved in water. A vacoule appears as an empty space under the microscope. All the plant cells have a large vacoule. The vacuole is filled with a liquid called "cell sap" , which contains dissolve sugar and salts. The function of vacuole in a cell is to store various substances including waste products of the cell.

* In amoeba vacuoles contain food particles so they are called food vacuoles.